Neural density matrix does not converge to exact solution for some models
Created by: GillianGrayson
I tried to find the steady-state for the many-body localization model from this paper: https://journals.aps.org/prb/abstract/10.1103/PhysRevB.98.020202 (arxiv link)
This is a dissipative model with the following Hamiltonian and Dissipators:
This model exists in half-filling subspace, so I used Hilbert space obtained as a tensor product of local Fock basis:
hi = Fock(n_max=1, n_particles=N//2, N=N)The number of states in this space is N choose N/2. This system (in such space) has a single unique steady state.
I tried to adapt your example of dissipative Ising 1D model but without any observables to track. I just wanted to check how the neural density matrix converges to the exact solution in terms of LdagL and norm of difference matrix (Exact minus NDM):
import netket as nk
import numpy as np
from numpy import linalg as la
import pandas as pd
from netket.hilbert import Fock
from tqdm import tqdm
# Model params
N = 8
seed = 1
W = 20.0
U = 1.0
J = 1.0
gamma = 0.1
# Ansatz params
beta = 2
alpha = 2
n_samples = 2000
n_samples_diag = 2000
n_iter = 500
np.random.seed(seed)
# Uniformly distributed on-site energies
energies = np.random.uniform(-1.0, 1.0, N)
# Hilbert space
hi = Fock(n_max=1, n_particles=N//2, N=N)
# The Hamiltonian
ha = nk.operator.LocalOperator(hi)
# List of dissipative jump operators
j_ops = []
for boson_id in range(N - 1):
ha += W * energies[boson_id] * nk.operator.boson.number(hi, boson_id)
ha += U * nk.operator.boson.number(hi, boson_id) * nk.operator.boson.number(hi, boson_id + 1)
ha -= J * (nk.operator.boson.create(hi, boson_id) * nk.operator.boson.destroy(hi, boson_id + 1) + nk.operator.boson.create(hi, boson_id + 1) * nk.operator.boson.destroy(hi, boson_id))
A = (nk.operator.boson.create(hi, boson_id + 1) + nk.operator.boson.create(hi, boson_id)) * (nk.operator.boson.destroy(hi, boson_id + 1) - nk.operator.boson.destroy(hi, boson_id))
j_ops.append(np.sqrt(gamma) * A)
ha += W * energies[N - 1] * nk.operator.boson.number(hi, N - 1) # Don't forget last term
# Create the Liouvillian
lind = nk.operator.LocalLiouvillian(ha, j_ops)
# Neural quantum state model: Positive-Definite Neural Density Matrix using the ansatz from Torlai and Melko
ndm = nk.models.NDM(
alpha=alpha,
beta=beta,
)
# Metropolis Local Sampling
sa = nk.sampler.MetropolisLocal(lind.hilbert)
# Optimizer
op = nk.optimizer.Sgd(0.01)
sr = nk.optimizer.SR(diag_shift=0.01)
# Variational state
vs = nk.vqs.MCMixedState(sa, ndm, n_samples=n_samples, n_samples_diag=n_samples_diag)
vs.init_parameters(nk.nn.initializers.normal(stddev=0.01))
# Driver
ss = nk.SteadyState(lind, op, variational_state=vs, preconditioner=sr)
metrics_dict = {
'iteration': np.linspace(1, n_iter, n_iter),
'ldagl_mean': [],
'ldagl_error_of_mean': [],
'norm_rho_diff': [],
}
# Calculate exact rho
rho_exact = nk.exact.steady_state(lind, method="iterative", sparse=True, tol=1e-10)
for it in tqdm(range(n_iter)):
out = ss.run(n_iter=1)
metrics_dict['ldagl_mean'].append(ss.ldagl.mean)
metrics_dict['ldagl_error_of_mean'].append(ss.ldagl.error_of_mean)
rho_neural = np.array(ss.state.to_matrix())
rho_diff = rho_exact - rho_neural
metrics_dict['norm_rho_diff'].append(la.norm(rho_diff))
metrics_df = pd.DataFrame(metrics_dict)
metrics_df.to_excel(f"metrics.xlsx", index=False)There are plots for LdagL and norm of difference matrix depend on number of iterations:
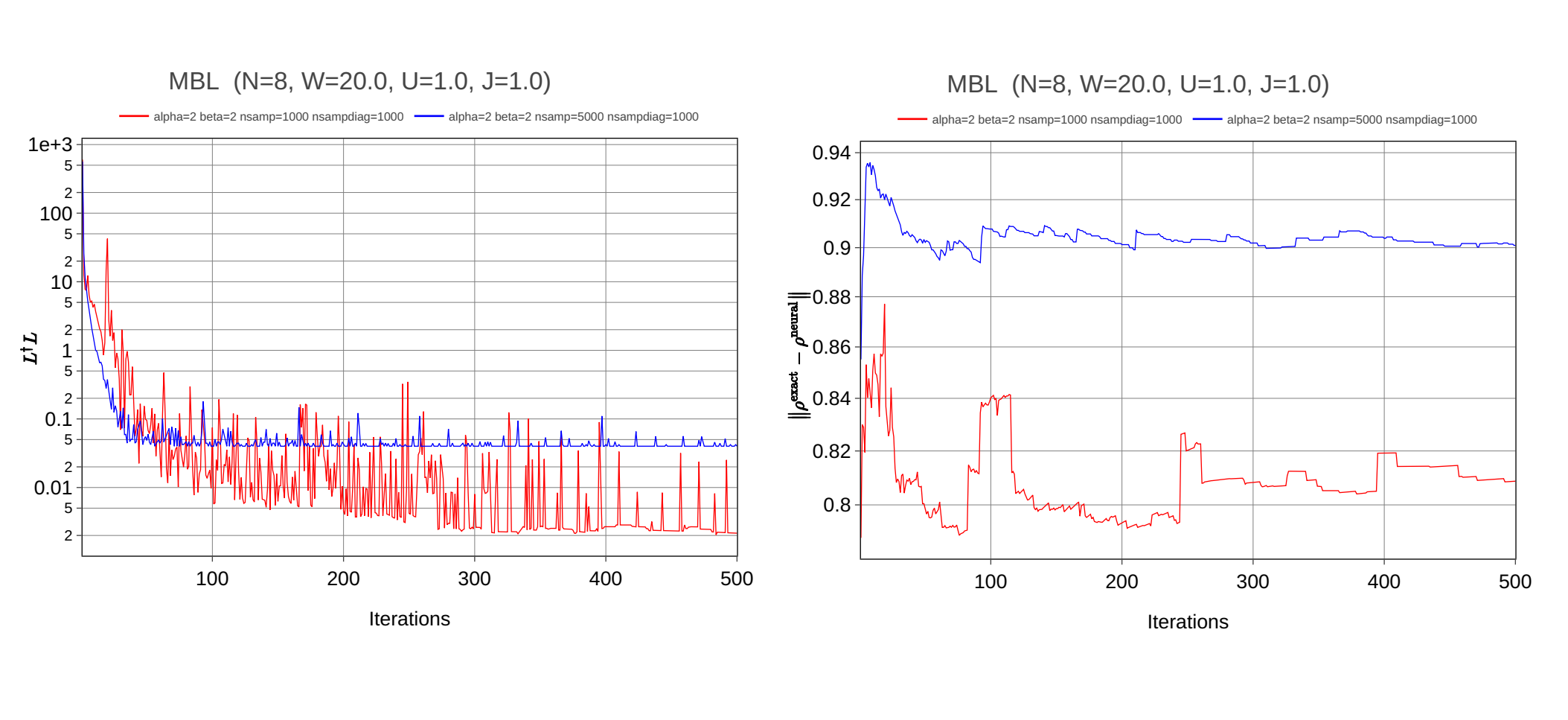
There are no converge to the exact solution in terms of the norm of difference matrix What am I doing wrong? Maybe I should use other types of samplers or I cannot combine Fock basis with NDM? Could you help me, please?
I also tried to observe the convergence for your example of dissipative Ising 1D model and everything is fine! Norm of difference matrix decreases with iterations:
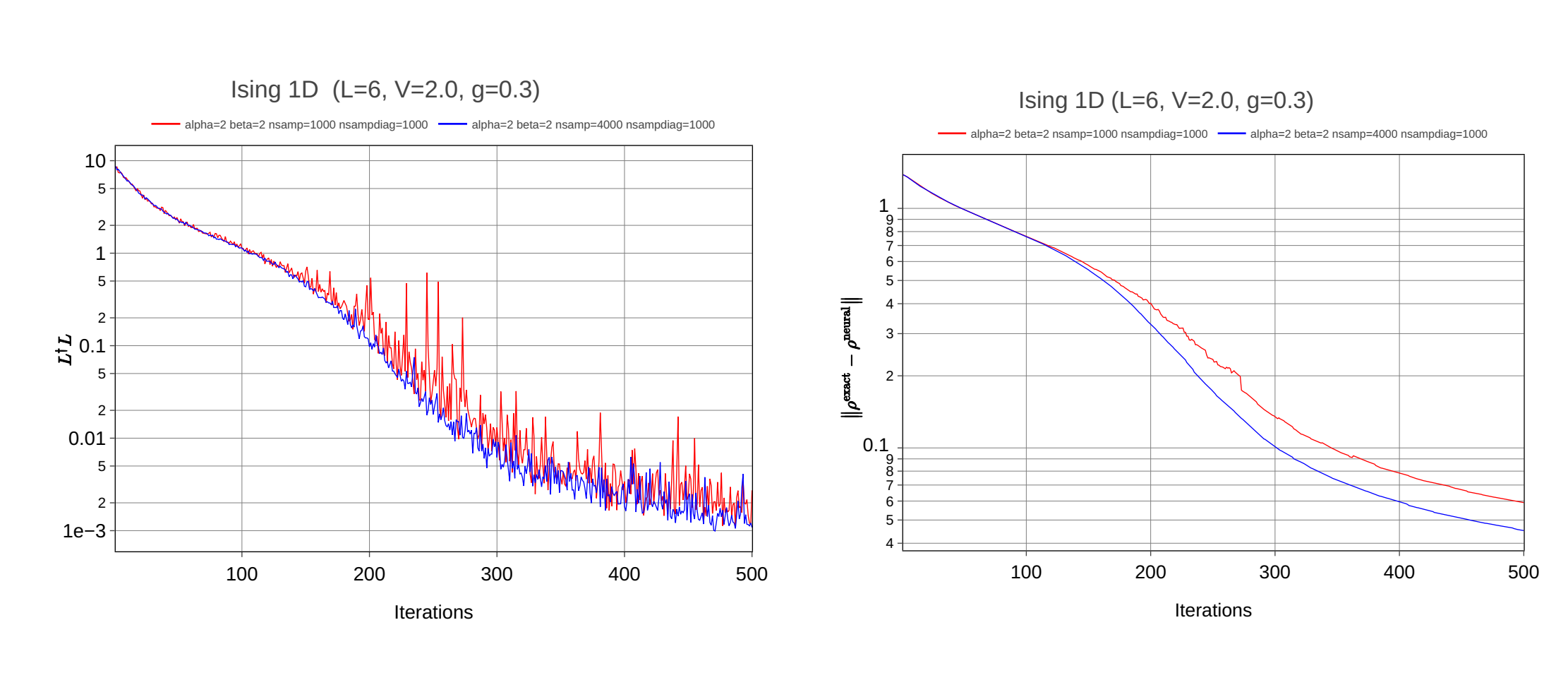
Also in both models I very often obtain errors something like:
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/netket/driver/abstract_variational_driver.py", line 251, in run
for step in self.iter(n_iter, step_size):
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/netket/driver/abstract_variational_driver.py", line 167, in iter
dp = self._forward_and_backward()
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/netket/driver/steady_state.py", line 124, in _forward_and_backward
self._dp = self.preconditioner(self.state, self._loss_grad)
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/netket/optimizer/preconditioner.py", line 74, in __call__
self.x0, self.info = self._lhs.solve(self.solver, gradient, x0=x0)
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/netket/optimizer/linear_operator.py", line 100, in solve
return self._solve(jax.tree_util.Partial(solve_fun), y, x0=x0, **kwargs)
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/netket/optimizer/qgt/qgt_jacobian_dense.py", line 136, in _solve
return _solve(self, solve_fun, y, x0=x0)
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/netket/optimizer/qgt/qgt_jacobian_dense.py", line 210, in _solve
out, info = solve_fun(unscaled_self, y, x0=x0)
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/jax/_src/scipy/sparse/linalg.py", line 278, in cg
return _isolve(_cg_solve,
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/jax/_src/scipy/sparse/linalg.py", line 218, in _isolve
x = lax.custom_linear_solve(
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/netket/optimizer/linear_operator.py", line 114, in __call__
return self @ vec
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/netket/optimizer/qgt/qgt_jacobian_dense.py", line 133, in __matmul__
return _matmul(self, vec)
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/netket/optimizer/qgt/qgt_jacobian_dense.py", line 171, in _matmul
mpi.mpi_sum_jax(((self.O @ vec).T.conj() @ self.O).T.conj())[0]
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/jax/_src/numpy/lax_numpy.py", line 5869, in deferring_binary_op
return binary_op(self, other)
File "/home/user/anaconda3/envs/py38/lib/python3.8/site-packages/jax/_src/numpy/lax_numpy.py", line 4219, in matmul
out = lax.dot_general(
TypeError: dot_general requires contracting dimensions to have the same shape, got [1696] and [3392].For example with the same parameters of MBL model but with changed parameters of Variational Anzats:
# Ansatz params
beta = 6
alpha = 6
n_samples = 5000
n_samples_diag = 1000
n_iter = 500How to fix it?
